|
1.Оценка параметров и структуры математической модели.
Задачи поиска оптимума возникают при построении математических моделей.
Когда для изучения какого-либо явления конструируется математическая модель, к оптимизации прибегают для того, чтобы определить ее структуру и параметры, которые обеспечивают наилучшее согласие с реальностью.
Пусть результат измерения случайной величины у зависит от  , причем , причем  где у - результат измерения,
где у - результат измерения,  - функция, вид которой известен, - функция, вид которой известен,  - неизвестные параметры функции. Оценка неизвестных параметров - неизвестные параметры функции. Оценка неизвестных параметров  при определенных условиях может быть произведена, например,
по методу наименьших квадратов посредством минимизации суммы квадратов при определенных условиях может быть произведена, например,
по методу наименьших квадратов посредством минимизации суммы квадратов

по  . Здесь N- количество наблюдений. . Здесь N- количество наблюдений.
Для определения структуры модели, т.е. определение ее вида, создается множество альтернативных моделей,
среди которых выбирается одна из моделей по некоторому критерию.
В качестве критерия может выступать либо сумма квадратов  ,
либо оценка дисперсии модели, либо коэффициент детерминации и т.п. ,
либо оценка дисперсии модели, либо коэффициент детерминации и т.п.
2. Задача Штейнера.
Классическая задача Штейнера формулируется так: требуется найти точку 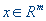 ,
сумма расстояний от которой до заданных точек ,
сумма расстояний от которой до заданных точек 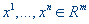 минимальна.
Эта задача типично оптимизационная: минимальна.
Эта задача типично оптимизационная:

Приведенные задачи представляют собой задачи безусловной оптимизации — на искомое решение не налагается никаких дополнительных условий, кроме того,
что оно должно доставлять минимум некоторой функции
(другими словами, минимум функции ищется на всем пространстве — области определения функции).
3. Задача о рационе.
Формулировка задачи о рационе: Пусть имеется n различных пищевых продуктов, содержащих m различных питательных веществ.
Обозначим через  долю j-го питательного вещества в i-ом продукте, через долю j-го питательного вещества в i-ом продукте, через 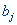 —
суточную потребность организма в j-ом питательном веществе,
через —
суточную потребность организма в j-ом питательном веществе,
через  — стоимость единицы i-го продукта.
Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных
веществах. Если обозначить через — стоимость единицы i-го продукта.
Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных
веществах. Если обозначить через  суточное потребление i-го продукта,
то эта задача может быть формализована следующим образом. Нужно минимизировать функцию суточное потребление i-го продукта,
то эта задача может быть формализована следующим образом. Нужно минимизировать функцию
 (стоимость рациона)
(стоимость рациона)
при условиях
 (рацион должен содержать не менее суточной потребности в каждом из питательных веществ).
(рацион должен содержать не менее суточной потребности в каждом из питательных веществ).
Очевидно, также следует требовать, чтобы

В векторных обозначениях задача о рационе может быть записана так: минимизировать функцию
f(x)=(c,x),
где  ; эту задачу, как обычно, мы записываем в виде
при ограничениях ; эту задачу, как обычно, мы записываем в виде
при ограничениях
 , ,
 . .
В них первое неравенство связывает два вектора Ax и b из  , а второе – два вектора x и , а второе – два вектора x и  из
из  . .
Стр.: 1, ..., 3
|
|
 Главная
Главная
 Классификация задач
Классификация задач
 Безусловная оптимизация
Безусловная оптимизация
 Условная оптимизация
Условная оптимизация
 Глоссарий
Глоссарий
 Карта сайта
Карта сайта
 , причем
, причем  где у - результат измерения,
где у - результат измерения,  - функция, вид которой известен,
- функция, вид которой известен,  - неизвестные параметры функции. Оценка неизвестных параметров
- неизвестные параметры функции. Оценка неизвестных параметров  при определенных условиях может быть произведена, например,
по методу наименьших квадратов посредством минимизации суммы квадратов
при определенных условиях может быть произведена, например,
по методу наименьших квадратов посредством минимизации суммы квадратов
 ,
либо оценка дисперсии модели, либо коэффициент детерминации и т.п.
,
либо оценка дисперсии модели, либо коэффициент детерминации и т.п. 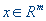 ,
сумма расстояний от которой до заданных точек
,
сумма расстояний от которой до заданных точек 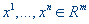 минимальна.
Эта задача типично оптимизационная:
минимальна.
Эта задача типично оптимизационная:
 долю j-го питательного вещества в i-ом продукте, через
долю j-го питательного вещества в i-ом продукте, через 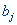 —
суточную потребность организма в j-ом питательном веществе,
через
—
суточную потребность организма в j-ом питательном веществе,
через  — стоимость единицы i-го продукта.
Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных
веществах. Если обозначить через
— стоимость единицы i-го продукта.
Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных
веществах. Если обозначить через  суточное потребление i-го продукта,
то эта задача может быть формализована следующим образом. Нужно минимизировать функцию
суточное потребление i-го продукта,
то эта задача может быть формализована следующим образом. Нужно минимизировать функцию
 (стоимость рациона)
(стоимость рациона)  (рацион должен содержать не менее суточной потребности в каждом из питательных веществ).
(рацион должен содержать не менее суточной потребности в каждом из питательных веществ).
 ; эту задачу, как обычно, мы записываем в виде
при ограничениях
; эту задачу, как обычно, мы записываем в виде
при ограничениях  ,
, .
. , а второе – два вектора x и
, а второе – два вектора x и  из
из  .
.