Методы Оптимизации Систем Автоматизированного Проектирования
 Главная
Главная
 Классификация задач
Классификация задач
 Безусловная оптимизация
Безусловная оптимизация
 Условная оптимизация
Условная оптимизация
 Глоссарий
Глоссарий
 Карта сайта
Карта сайта
|
Обе штрафные функции определены и непрерывны внутри множества G , т.е. на множестве
Начальная точка поиска задается только внутри множества допустимых решений G. На каждой k-й итерации ищется точка
Вычисления прекращают при выполнении условий:
Алгоритм. Шаг 1. Задать начальную точку внутри области G, внутри области G,  для уменьшения параметра для уменьшения параметра
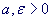 для остановки алгоритма. Положить k=0. для остановки алгоритма. Положить k=0.
Шаг 2. Составить вспомогательную функцию: 
Шаг 3. Найти точку 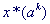 минимума функции минимума функции 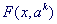 по x с помощью какого-либо
метода безусловной оптимизации
(нулевого, первого или второго порядка) с проверкой принадлежности текущей точки внутренности множества G: по x с помощью какого-либо
метода безусловной оптимизации
(нулевого, первого или второго порядка) с проверкой принадлежности текущей точки внутренности множества G:
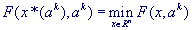
В качестве начальной точки берется точка 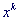 . .
Вычислить 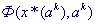 . .
Шаг 4. Проверить условие окончания: а) если 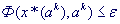 , процесс поиска закончить: , процесс поиска закончить:
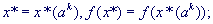
б) если 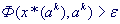 , положить , положить  перейти к шагу 2. перейти к шагу 2.
|
 Методы штрафных функций:
Методы штрафных функций:
-Общие сведения
-Метод внешних штрафных функций
-Метод внутренних штрафных функций
 Методы возможных направлений:
Методы возможных направлений:
-Общие сведения
-Основные определения
-Построение возможных направлений спуска
-Метод Зойтендейка
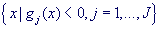 и стремятся к бесконечности при приближении к границе множества изнутри. Поэтому они называются барьерными функциями. При
и стремятся к бесконечности при приближении к границе множества изнутри. Поэтому они называются барьерными функциями. При
 штрафная функция, задаваемая обратной функцией, положительна. Логарифмическая штрафная функция положительна при -1 < g(x) < 0 и отрицательна при g(x) < -1, т.е. внутренним точкам области отдается предпочтение перед граничными.
штрафная функция, задаваемая обратной функцией, положительна. Логарифмическая штрафная функция положительна при -1 < g(x) < 0 и отрицательна при g(x) < -1, т.е. внутренним точкам области отдается предпочтение перед граничными.
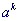 с помощью какого-либо метода безусловной оптимизации (нулевого, первого или второго порядка). Полученная точка
с помощью какого-либо метода безусловной оптимизации (нулевого, первого или второго порядка). Полученная точка
 последовательность
последовательность 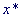 .
Барьерные функции как бы препятствуют выходу из множества G, а если решение находится на границе, то метод приводит к движению изнутри области к границе.
.
Барьерные функции как бы препятствуют выходу из множества G, а если решение находится на границе, то метод приводит к движению изнутри области к границе.

 - заданные числа, определяющие точность вычислений.
- заданные числа, определяющие точность вычислений.