Методы Оптимизации Систем Автоматизированного Проектирования

Пример 2.

Пусть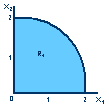

Хотя допустимое множество решений и выпукло, но число крайних точек здесь бесконечное.

Для решения большинства практических задач используются численные методы, которые делятся на две группы:

1. Методы, использующие преобразование задачи НП в последовательность задач безусловной оптимизации путем построения вспомогательных функций – методы последовательной безусловной минимизации.

2. Методы непосредственного решения задачи НП, основанные на движении из одной допустимой точки, где выполняются все ограничения, к другой допустимой точке с лучшим значением целевой функции – методы возможных направлений.

Основная идея методов первой группы состоит в том, чтобы аппроксимировать исходную задачу НП некоторой вспомогательной задачей, решение которой можно получить стандартными методами. Естественно, что ограничившись одной вспомогательной задачей, можно получить, вообще говоря, лишь приближенное решение исходной задачи. Если использовать последовательность задач, в некотором смысле «сходящуюся» к исходной, то искомое точное решение в большинстве случаев окажется пределом соответствующей последовательности приближенных решений.

К методам первой группы относятся метод внешних штрафных функций и метод внутренних штрафных функций (метод барьеров). В первом методе к целевой функции добавляется функция, интерпретируемая как штраф за нарушение каждого из ограничений. Метод генерирует последовательность точек, которая сходится к решению исходной задачи.

Во втором методе к целевой функции добавляется слагаемое, которое не позволяет генерируемой последовательности точек выходить за пределы допустимой области.

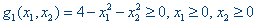
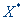Методы, образующие вторую группу, связаны с нахождением предела последовательности 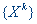допустимых точек при , таких, что 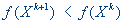, k=0,1,...К данной группе методов относится метод возможных направлений Зойтендейка.

Стр.: 1, ...